Markov Chains are fundamental mathematical processes that are applied to problem solving in many different fields. They look into dependant variables, where the next position in the chain is only reliant on the current position.
This report investigates the representation of Markov Chains through random mapping and examples of random walks. As well as exploring the proofs behind the existence and uniqueness of a stationary distribution – a key component behind the workings of Markov Chains, we also delve into the world of Markov Chain Monte Carlo, as well as how Markov Chains can be applied to the real world.
.
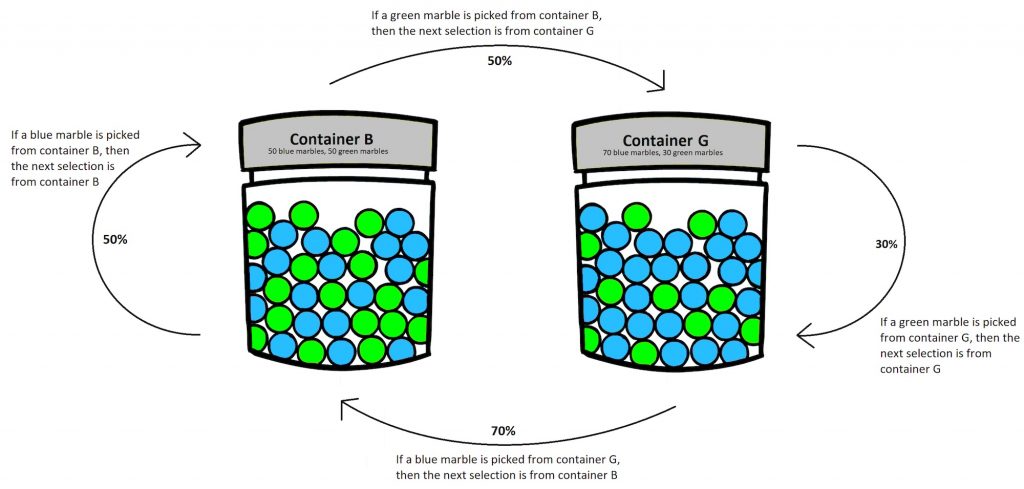
Developed by Siobhan Dobie
